
こんにちは、ヒガシです。
このページではPythonを使って、ねじれの位置にある2本の直線の最短距離(共通垂線の長さ)を計算する方法をご紹介していきます。
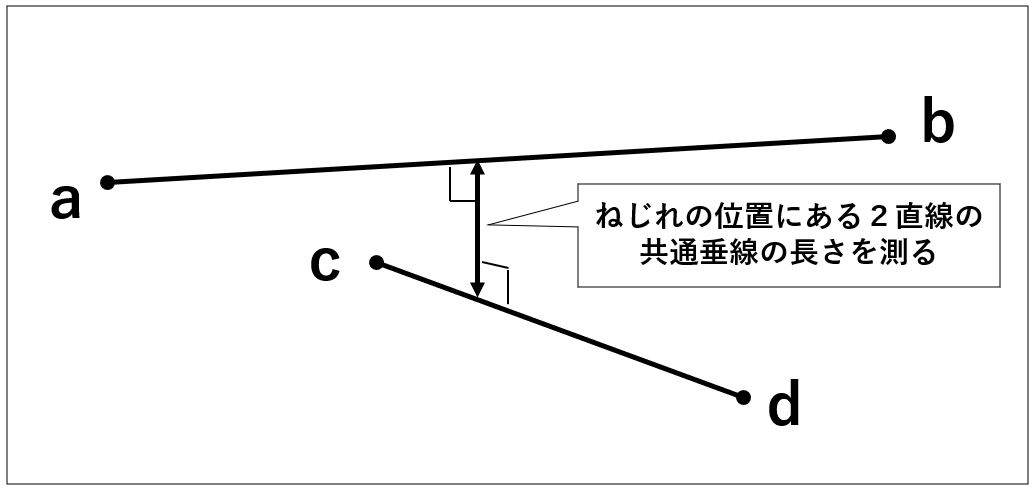
基本的にあなたがやることは上の画像に示すようにそれぞれの線を構成する2点の座標(a,b,c,d)を指定するだけでOKです。
それではさっそくやっていきましょう!
ねじれの位置にある2直線の最短距離の計算方法
ねじれの位置にある2直線の最短距離を計算する方法については以下のサイトが非常に参考になりましたので掲載しておきます。

今回は計算結果が正解かどうか確認するために上記参考サイトと全く同じ2本の線に対して計算を実施していきます。
なお、数学的に計算する場合は上記サイトのように計算していけばいいですが、コンピューターがこの計算をするのはあまり得意ではありません。
というわけここからは、コンピュータ上で今回やりたい計算を実施する方法をざっくり解説していきます。
イメージは以下の通りです。
①まずは適当にそれぞれの直線上に点を置き、両者の距離を計測します。
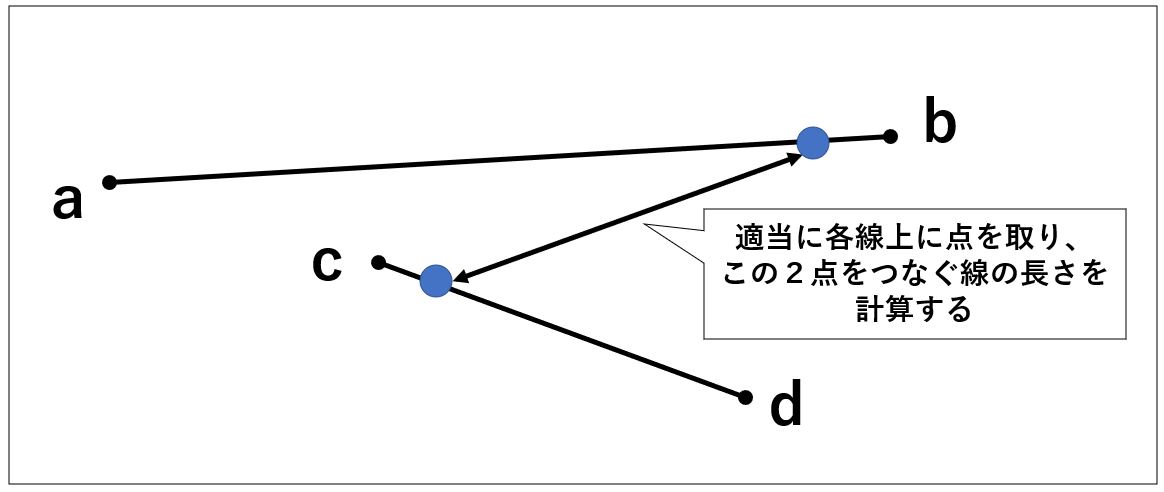
②それぞれの点をすこしだけ動かしてまた距離を計算します。
これを何度も繰り替えし、最短距離を探していく作業をおこなっていきます。
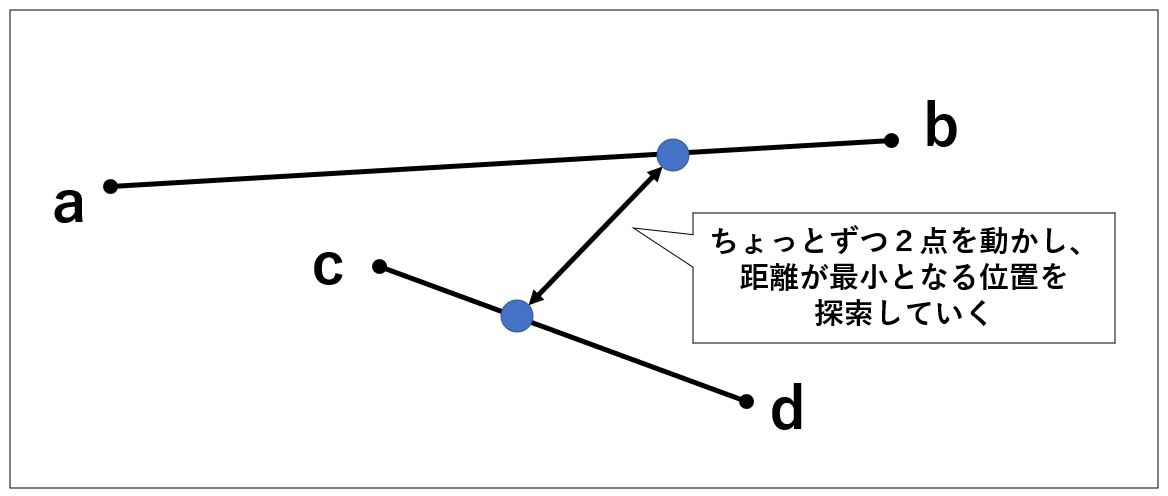
まぁ難しいことは考えず、いったんコーディングしてみましょう。
Pythonで共通垂線の長さを計算するサンプルコード
それではさっそくですが、サンプルコードのご紹介です。
#ライブラリインポート
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#ab,cdでそれぞれ繋がる2直線の最短距離を計算する
#参照(https://math-juken.com/kijutu/kyoutusuisen/)
a=[0,0,0]
b=[1,2,3]
c=[4,5,-6]
d=[7,8,9]
line1=[a,b]
line2=[c,d]
#2直線の距離を計算する関数
def calc_distance(s,t):
a,b=line1[0],line1[1]
c,d=line2[0],line2[1]
ABbec=np.array([b[0]-a[0],b[1]-a[1],b[2]-a[2]])
CDbec=np.array([d[0]-c[0],d[1]-c[1],d[2]-c[2]])
PQbec=(c+CDbec*s)-(a+ABbec*t)
distance=np.linalg.norm(PQbec)
return distance
#2直線の距離を探索する関数
def make_map(ss,tt):
z_list=[]
ij_list=[]
for i in range(len(ss)):
for j in range(len(tt)):
s,t=ss[i],tt[j]
z=calc_distance(s,t)
z_list.append(z)
ij_list.append([i,j])
return z_list,ij_list
#大きな範囲で最小値をざっくり探索
ini_max=2000
ini_min=-2000
delta=200
ss=np.linspace(ini_min,ini_max,delta)
tt=np.linspace(ini_min,ini_max,delta)
z,ij=make_map(ss,tt)
min_val=np.amin(np.array(z))
min_index=z.index(min_val)
#範囲を狭めながら最小値を繰り返し計算
minz_list=[]
for k in range(7):
i,j=ij[min_index][0],ij[min_index][1]
smax,smin=min(ss[i+2],ini_max),max(ss[i-2],ini_min)
tmax,tmin=min(tt[j+2],ini_max),max(tt[j-2],ini_min)
ss=np.linspace(smin,smax,delta)
tt=np.linspace(tmin,tmax,delta)
z,ij=make_map(ss,tt)
min_val=np.amin(np.array(z))
min_index=z.index(min_val)
minz_list.append(min_val)
print('min_distance=' + str(min_val))
#正解データの計算(https://math-juken.com/kijutu/kyoutusuisen/)
P=np.array([5,10,15])
Q=np.array([73,82,131])/9
PQ=P-Q
print('answer=' +str(np.linalg.norm(PQ)))
非常に長いですが、基本的にあなたがやることは8~11行目のa,b,c,d各点の座標を入力するだけでOKです。
サンプルコードの実行結果確認
それでは先ほどのコードを実行してみましょう。
※先ほど紹介した参考サイトにて算出された正解データもあわせて表示するようにしてます。Python上で算出した結果はmin_distance=で表示されている部分です。
先ほどのコードを実行すると以下の結果が得られました。
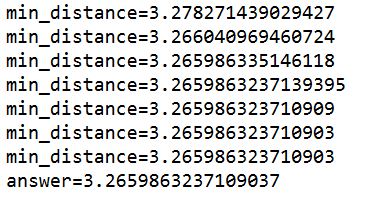
min_distanceというのが何度も表示されていますが、これが先ほど紹介したように点をちょっとずつ動かして最短距離を探索している過程になります。
少しずつある値に近づいていることがわかると思います。
また、最後のanswerが先述したとおり、以下のサイトの結果をつかって計算したものです。

今回はあくまでも探索的に求めたので数学的に求めた結果とは若干ずれていますが、ほぼ同じ結果を出力することができていますね。

工学分野にいる私としてはこのくらい精度があれば十分ですね。
プログラム実行上の注意点
今回はあくまでも適当に探索する範囲を決めたうえで実行しています。
(コードでいうと42~44行目あたり)
なので最短距離を形成する点が探索範囲にない場合はうまく計算することができません。
もし値が収束しない等の問題が出た場合は探索範囲を修正してみることをオススメします。
おわりに
というわけで今回はPythonを使って、ねじれの位置にある2直線の最短距離を計算する方法をご紹介しました。
空間設計の際などにぜひご活用ください。
このように、私のブログでは様々なスキルを紹介しています。
今は仕事中で時間がないかもしれませんが、ぜひ通勤時間中などに他の記事も読んでいただけると嬉しいです。
⇒興味をもった方は【ヒガサラ】で検索してみてください。
確実にスキルアップできるはずです。
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
![]()
にほんブログ村
それではまた!
Follow @HigashiSalary




コメント